Develop New Discretization for Solving Fluid Flows
The current approach in improving the flow solver performance is very close to stagnation point. In order to further improve it we need a new paradigm.
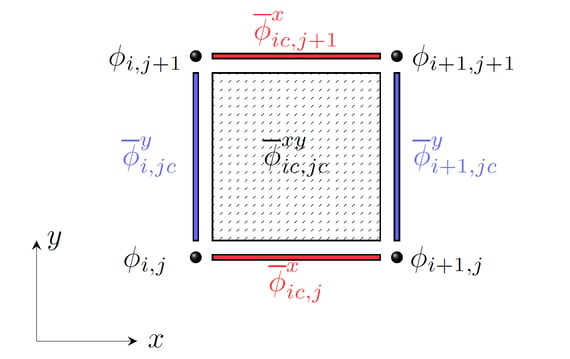
Our proposal is to combine the existing discretization method namely: FDM, FVM, and the newly developed FSM to solve the fluid flow simultaneously. This approach allow us to capture the very fine detail of the flow field using the standard traditional Cartesian grid. This multi-moment method is a natural evolution of the Lele's compact scheme in 1993 [1], the compact finite volume in 2010 [2], and the finite surface method in 2020 [3].
[1] https://doi.org/10.1016/0021-9991(92)90324-R
[2] https://doi.org/10.1016/j.jcp.2010.05.042
[3] https://doi.org/10.1016/j.jcp.2020.109790
Qualifications
Obtained Master's degree or first class honors ( eqv 3.5/4.0 system)
Solid background in mathematics and physics
Proficiency in Fortran, Python, and MATLAB
Determined and self-motivated
Love numerics
Expecations
You will be working 18h with us (online of onsite)
You will be engaged in several projects concurrently
Renumeration 300 - 600 USD depending on the number of projects
You will be enroll in our Ph.D. or Master's program.
Additional Scolarships
These scholarships provided 300-400USD living allowance per month. The president's scholarships waive the tuition fee.
